城市給水管網(wǎng)可靠度的計(jì)算
| 論文類型 | 技術(shù)與工程 | 發(fā)表日期 | 2002-04-01 |
| 來源 | 《中國(guó)給水排水》2002年第4期 | ||
| 作者 | 趙新華,劉英梅,喬宇 | ||
| 關(guān)鍵詞 | 城市給水管網(wǎng) 可靠度 最小路 不交化 | ||
| 摘要 | 研究了城市給水管網(wǎng)可靠度的計(jì)算,首先從可靠度與圖論原理出發(fā),闡釋了算法設(shè)計(jì)的依據(jù),然后從管網(wǎng)結(jié)構(gòu)的角度,以最小路原理為依據(jù),應(yīng)用最小路不交化方法設(shè)計(jì)了給水管網(wǎng)可靠度的算法并進(jìn)行了實(shí)例驗(yàn)證。 | ||
趙新華1, 劉英梅1, 喬 宇2
( 1.天津大學(xué)環(huán)境科學(xué)與工程學(xué)院,天津300072;2.天津大學(xué)機(jī)械學(xué)院,天津 300072)
摘 要:研究了城市給水管網(wǎng)可靠度的計(jì)算,首先從可靠度與圖論原理出發(fā),闡釋了算法設(shè)計(jì)的依據(jù),然后從管網(wǎng)結(jié)構(gòu)的角度,以最小路原理為依據(jù),應(yīng)用最小路不交化方法設(shè)計(jì)了給水管網(wǎng)可靠度的算法并進(jìn)行了實(shí)例驗(yàn)證。
關(guān)鍵詞:城市給水管網(wǎng);可靠度;最小路;不交化
中圖分類號(hào):TU991.33
文獻(xiàn)標(biāo)識(shí)碼:C
文章編號(hào):1000-4602(2002)04-0053-03
? 以最小路不交化算法為核心,從管網(wǎng)的網(wǎng)絡(luò)系統(tǒng)結(jié)構(gòu)入手,分析管段的關(guān)聯(lián)關(guān)系對(duì)管網(wǎng)可靠度的影響,采用遍歷計(jì)算的方式,從單個(gè)管段的可靠度計(jì)算出管網(wǎng)中水源點(diǎn)與任意非水源點(diǎn)的可靠度,取最小值作為管網(wǎng)系統(tǒng)可靠性的評(píng)價(jià)。
1 計(jì)算依據(jù)
如果給定一個(gè)網(wǎng)絡(luò),將其整體作為一個(gè)系統(tǒng)、每條弧作為一個(gè)組件。系統(tǒng)可靠性理論的中心問題是要確定系統(tǒng)可靠度與其組件可靠度之間的關(guān)系。?
1.1 管網(wǎng)組件可用度A
給水管網(wǎng)在實(shí)際運(yùn)行中經(jīng)常出現(xiàn)管段故障的情況,經(jīng)維修后仍投入正常運(yùn)行,那么稱這樣的管段為可維修組件,其可靠度用組件可用度A表示。?
組件在規(guī)定的條件下,在任意時(shí)刻上正常工作的概率稱為組件瞬時(shí)可用度A(t);與瞬時(shí)可用度相對(duì)應(yīng)的是瞬時(shí)不可用度,表示組件在規(guī)定的條件下使用時(shí)任意時(shí)刻故障的概率用Q(t)表示,顯然Q(t)=1-A(t)。?
采用組件瞬時(shí)可用度公式:?
![]()
式中 ?λ——管網(wǎng)的故障率?
μ——管網(wǎng)的修復(fù)率?
將組件可用度A定義為管段從開始到使用壽命T這一時(shí)間段內(nèi)的平均可用度,即求A(t)的數(shù)學(xué)期望E[A(t)]。由函數(shù)的數(shù)學(xué)期望公式得:?
![]()
又因?yàn)閒(t)在[0,T]時(shí)間段內(nèi)服從均勻分布,f(t)=1/T、t∈[0,T],故組件可用度的數(shù)學(xué)式表示為:
![]()
相應(yīng)的組件不可用度Q=1-A。?
1.2 管網(wǎng)系統(tǒng)可靠度
在研究系統(tǒng)可靠性時(shí),首先對(duì)所研究的對(duì)象作4點(diǎn)假設(shè):?
① 組件和系統(tǒng)都只有正常和失效兩種狀態(tài);?
② 系統(tǒng)的狀態(tài)完全由系統(tǒng)的邏輯關(guān)系和組件的狀態(tài)決定;?
③ 組件的狀態(tài)轉(zhuǎn)移率即故障率λ和修復(fù)率μ均為常數(shù);?
④ 組件或系統(tǒng)的故障和修復(fù)都相互獨(dú)立。?
采用最小路不交化算法求解。設(shè)G是一個(gè)給定的網(wǎng)絡(luò),V1、V2是指定的兩個(gè)節(jié)點(diǎn),則基本問題是求時(shí)刻T由輸入節(jié)點(diǎn)V1可以到達(dá)輸出節(jié)點(diǎn)V2的概率,亦即求時(shí)刻T系統(tǒng)正常的概率R。?
對(duì)網(wǎng)絡(luò)的路及最小路的定義如下:?
定義1對(duì)于給定網(wǎng)絡(luò)G,從指定的節(jié)點(diǎn)V1經(jīng)過一串弧序列(或其中的一部分弧)可以到達(dá)節(jié)點(diǎn)V2,則稱這個(gè)弧序列為從V1到V2的一條路。?
定義2對(duì)于給定網(wǎng)絡(luò)G,從節(jié)點(diǎn)V1到V2的弧序列稱作一條最小路,若滿足①它是一條路,②最小性,即從這個(gè)弧序列中除去任意一條弧后它即不是從V1到V2的路。?
由于系統(tǒng)正常這一事件可表示為S={V1可以到達(dá)V2}={由V1至少有一條最小路通到V2},這里最小路是指組成這條最小路的弧都正常這一事件。因此,若記A1,A2,…,Am為網(wǎng)絡(luò)的所有最小路,則![]() ,,即將求可靠度問題轉(zhuǎn)化為求隨機(jī)事件和的問題。?
,,即將求可靠度問題轉(zhuǎn)化為求隨機(jī)事件和的問題。?
由概率論可知:![]() 稱為容斥定理 。?
稱為容斥定理 。?
若能把系統(tǒng)正常這一事件表示成不交(即相斥)事件之和![]() 稱為相斥求和公式。?
稱為相斥求和公式。?
當(dāng)最小路數(shù)目不多時(shí),用直觀方法可以得到全部最小路;若系統(tǒng)結(jié)構(gòu)復(fù)雜,產(chǎn)生的最小路數(shù)目較多時(shí),應(yīng)采用圖論中的鄰接矩陣法[1、2]求全部最小路。用最小路不交化方法將相依事件轉(zhuǎn)化為相斥事件,然后利用相斥求和公式求解系統(tǒng)的可靠度,從而簡(jiǎn)化了計(jì)算過程。?
定理1設(shè)A1,KAm為網(wǎng)絡(luò)G的所有最小路,A1,L,Ar的長(zhǎng)度都小于n-1,Ar+1,L,Am的長(zhǎng)度為n-1,且r<m,則:
![]()
其中右端![]() 、Br+1、L、Bm之間不交,而Br+1、L、Bm為Ar+1、L、Am中分別添上在其中不出現(xiàn)的(l-n+1) 條弧的逆而成之事件。?
、Br+1、L、Bm之間不交,而Br+1、L、Bm為Ar+1、L、Am中分別添上在其中不出現(xiàn)的(l-n+1) 條弧的逆而成之事件。?
2 算法設(shè)計(jì)
對(duì)于已知結(jié)構(gòu)的管網(wǎng)系統(tǒng),每個(gè)水源點(diǎn)與每個(gè)非水源點(diǎn)之間的系統(tǒng)可靠度都可以采用最小路不交化算法求得,即:將水源點(diǎn)處理為輸入節(jié)點(diǎn),非水源點(diǎn)處理為輸出節(jié)點(diǎn),采用鄰接矩陣法求得網(wǎng)絡(luò)的所有最小路,并對(duì)所求得的所有最小路進(jìn)行不交化處理,就可以結(jié)合組件的可用度進(jìn)行此時(shí)的系統(tǒng)可靠度計(jì)算。?
假設(shè)管網(wǎng)的管段可用度Ax與管段不可用度Qx均已求出,且通過鄰接矩陣分析已知A1,KAm為管網(wǎng)G中水源點(diǎn)i與非水源點(diǎn)j之間的所有最小路,A1,L,Ar的長(zhǎng)度都小于n-1,Ar+1、L、Am的長(zhǎng)度為n-1,則其系統(tǒng)可靠度R的計(jì)算過程如下:
① 挑出長(zhǎng)度為n-1的最小路全體Ar+1、KAm,利用公式![]() 將求集合并的問題簡(jiǎn)化為求代數(shù)和的形式,Bi是指在Ai中添上在其中不出現(xiàn)的(l-n+1)條弧的逆而成之事件,Bi之間不交,其概率之和作為系統(tǒng)可靠度的一部分,即最小路長(zhǎng)度為n-1子集的可靠度R1。?
將求集合并的問題簡(jiǎn)化為求代數(shù)和的形式,Bi是指在Ai中添上在其中不出現(xiàn)的(l-n+1)條弧的逆而成之事件,Bi之間不交,其概率之和作為系統(tǒng)可靠度的一部分,即最小路長(zhǎng)度為n-1子集的可靠度R1。?

循環(huán)計(jì)算,其中每一步使Aj與A1、L、Aj-1、不交,j=2,……,r(r為集合元素?cái)?shù))。
d.?F中還有項(xiàng)(即rk+1≥1)嗎?若有,則K←K+1,轉(zhuǎn)b步驟),否則結(jié)果R2就作為系統(tǒng)可靠度的另一部分。
③ R=R1+R2即為系統(tǒng)可靠度,任一條不交化最小路Bi=x1Lxn-1xnLxl的概率為:P{Bi}=Ax1LAxn-1QxnLQxl。
在分別考慮了每個(gè)非水源點(diǎn)與水源點(diǎn)之間的系統(tǒng)可靠度后,給水管網(wǎng)的可靠度取其中的最小值,即最不利點(diǎn)的系統(tǒng)可靠度。?
3 實(shí)際算例
某市一小區(qū)給水管網(wǎng)的規(guī)劃設(shè)計(jì),管網(wǎng)共有20個(gè)節(jié)點(diǎn),其中有一個(gè)水源點(diǎn)、19個(gè)用水點(diǎn)和28條管段(見圖1),設(shè)計(jì)供水能力為131 L/s左右,全部管段采用DN100~DN500的鑄鐵管鋪設(shè)。?
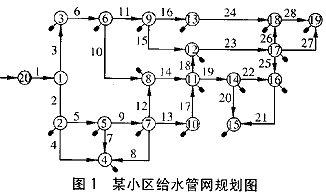
故障率λ定義為單位時(shí)間單位長(zhǎng)度管線發(fā)生故障的次數(shù)。對(duì)該市多年的經(jīng)驗(yàn)數(shù)據(jù)進(jìn)行統(tǒng)計(jì),確定的管道故障率λ值見表1。
修復(fù)率μ定義為單位時(shí)間管道維修的次數(shù)。根據(jù)該市大量管道維修業(yè)務(wù)臺(tái)帳進(jìn)行統(tǒng)計(jì),對(duì)于DN300及DN300以下的管道修復(fù)率取1095次/a,對(duì)于DN300以上的管道修 復(fù)率取730次/a。
本算例采用的時(shí)間段T值為5 A,從計(jì)算結(jié)果(表2)可見該小區(qū)的管網(wǎng)很可靠,即管段比較可靠和管網(wǎng)的網(wǎng)絡(luò)結(jié)構(gòu)合理。在管網(wǎng)的運(yùn)行中各個(gè)管段相互關(guān)聯(lián),后者對(duì)于管網(wǎng)的改擴(kuò)建工作尤其有重要意義,因?yàn)樵诓贿^多改變管徑的前提下,通過提高管網(wǎng)的連通性來提高管網(wǎng)的可靠性是既節(jié)約成本又保證管網(wǎng)可靠性的好方法。
4 結(jié)語
從管網(wǎng)靜態(tài)結(jié)構(gòu)出發(fā)計(jì)算了管網(wǎng)系統(tǒng)的可靠度,并利用實(shí)際管網(wǎng)的結(jié)構(gòu)參數(shù)進(jìn)行了驗(yàn)證,證明了算法的有效性,但還需進(jìn)一步研究的問題如下:?
① 改進(jìn)現(xiàn)有算法,引入稀疏矩陣、并行計(jì)算等方法以提高運(yùn)算速度,利于大型管網(wǎng)的計(jì)算研究。?
② 結(jié)合管網(wǎng)運(yùn)行的動(dòng)態(tài)性計(jì)算管網(wǎng)的水力可靠度,但是水力可靠度的分析與結(jié)構(gòu)可靠度的分析是密不可分的,需要找到它們之間的綜合關(guān)系,進(jìn)行管網(wǎng)系統(tǒng)可靠性的整體評(píng)價(jià)。?
③ 若把可靠度的計(jì)算與管網(wǎng)改擴(kuò)建工作的綜合規(guī)劃相結(jié)合,將發(fā)揮更大的作用。
參考文獻(xiàn):
[1]阿布拉莫夫H H.給水系統(tǒng)可靠性[M].北京:中國(guó)建筑工業(yè)出版社,1990.
[2]Rajesh Gupta.Reliability analysis of water-distribution systems[J].Journal of Environmental Engineering,120(2):447-460.
[3]Bao Y,Mays L W.Model for water-distribution system reliability[J].Journal of Hydraulic Engineering,116(11):1119-1137.
電 話:(022)27400830
收稿日期:2001-10-11
論文搜索
月熱點(diǎn)論文
論文投稿
很多時(shí)候您的文章總是無緣變成鉛字。研究做到關(guān)鍵時(shí),試驗(yàn)有了起色時(shí),是不是想和同行探討一下,工作中有了心得,您是不是很想與人分享,那么不要只是默默工作了,寫下來吧!投稿時(shí),請(qǐng)以附件形式發(fā)至 paper@h2o-china.com ,請(qǐng)注明論文投稿。一旦采用,我們會(huì)為您增加100枚金幣。








